Difference between revisions of "基于物理的BRDF"

Revision as of 23:52, 1 January 2011 (view source) Gongminmin (Talk | contribs) m Newer edit →

(No difference)

---

Revision as of 23:52, 1 January 2011

引言

基于物理的渲染已经提出好多年了，但在游戏中使用的渲染模型仍然是拼凑出来的经验公式（比如Phong）。这些拼凑的模型如果要渲染高质量的图像， 就需要繁复地调参数。而基于物理的、保能量的渲染模型可以很容易地建立出在不同光照环境下都接近真实的材质来。

神奇的是，基于物理的模型并不会比传统上拼 凑的模型更难实现，计算量也差不多。

反射方程

游戏中最常使用的渲染模型描述的是反射，不考虑SSS等。反射方程可以表示成：

其中，ρ(l, v)表示BRDF，L_i(l)表示光源给的贡献，(n · l)表示光源和表面法线的夹角。这个积分的结果就是所有光源对一个点的贡献之和。

Diffuse项

最简单的一个BRDF就是Lambert，在游戏中就是用(n · l)来表示。但实际上，(n · l)是属于反射方程的一项，而Lambert则是一个常量：

精确光源

游戏中经典的光源有point, directional和spot，这些局部光源都可以抽象成“精确光源”的概念，表示一个方向确定、大小为无穷小的光源。由于要计算的是到达表面点时的光照，所以不考虑从光源到表面之间的衰减。因此，精确光源都可以用颜色c_light和光源方向向量l_c这两个参数来表示。光源颜色c_light的确切定义是，白色的Lambert表面被平行于表面法线（l_c = n）的光照照亮的颜色。

如何计算这个光源对点的贡献呢？这里需要先引入一个叫做微面光源的概念。顾名思义，微面光源是一个非常小的面光源，中心是l_c，张角是ε。该微面光源照亮表面的一个点可以用L_tiny(l)来表示。它有两个性质：

第一个性质表示如果入射方向和l_c的夹角大于ε， 那么亮度为0。第二个性质是从c_light的定义而来，白色表面使得c_diff = 1，结合上文所说的反射方程和Lambert，就可以得出性质二。由于c_light要求l_c = n，所以c_light也表示了当ε趋近于0的时候的极限，也就是

因为l_c = n而且ε→0，我们可以认为(n · l) = 1，所以得到：

也就是

把微面光源带入一般的BRDF，得到的就是当趋近于0时的极限：

所以

入你所见，刚才引入的微面光源已经从公式中消失，剩下的部分又回到了熟悉的几个项。

Microfacet BRDF

大多数基于物理的specular BRDF的基础是microfacet理论。这个理论是用来描述来自于一般表面（不是光学平滑的）的反射。Microfacet理论的基本假设是，表面是由很多微平面（microfacet）组成，这些微平面都太小了，没有办法一个一个地看到；并假设每个microfacet都是光学平滑的。

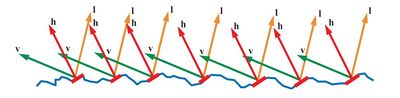
每个microfacet把一个入射方向的光反射到单独的一个出射方向，这取决于microfacet的法向m。当计算BRDF的时候，光源方向l和视线方向v都得给定。这意味着在表面上的所有microfacet中，只有刚好把l反射到v的那部分对BRDF有贡献。在下图中，我们可以看到这些有效microfacet的表面法向m正好在l和v的中间，也就是h。

并不是所有m = h的microfacet对反射都有贡献。有些microfacet会在光源方向l被其他microfacet阻挡（shadowing），有些会在视线方向v被阻挡（masking），也可能都有。Microfacet理论假设所有被遮挡的没有对BRDF的贡献。Microfacet的specular BRDF可以表达成：

F(l, h)是有效microfacet（m = h）产生的Fresnel反射。G(l, v, h)是有效microfacet中没有被shadow或mask的比例。D(h)是microfacet的法线分布函数，或者说，microfacet的法线等于h的密度。最后，分母4(n · l)(n · v)是个校正因子，用来校正从microfacet的局部空间转到整体表面的数量差异。

Fresnel项

Fresnel反射项计算从光学平滑的表面反射的比率。它的值取决于两件事情：入射角（光源方向和表面法线之间的角），以及材质的折射率。Schlick近似的Fresnel项是：

其中c_spec是specular颜色。

法线分布项

在大部分表面上，microfacet的方向不是均匀分布的。Microfacet的法线越接近宏表面的法线，就越光滑。这个分布由microfacet的法线分布函数D(m)来定义。函数D()决定了specular高光的大小、亮度和形状。 法线分布函数一般有类似于“粗糙度”这样的参数（各向异性的函数通常有两个参数）。

遮挡项（shadowing-masking term）

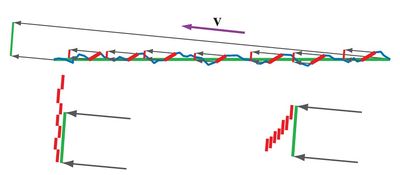
遮挡项G(l, v, h)也经常称为几何项。在很多情况下，遮挡项在某种程度上抵消了microfacet方程中的(n · l)(n · v)分母，替换成类似于max(n · l, n · v)这样的形式。遮挡项对BRDF保能量是很重要的——没有这个项的话，BRDF反射出的能量可能比接收到的更多。 Microfacet BRDF中很重要的一个事情是把能量从l反射到v的microfacet面积之和（有效面积）和宏表面总面积之间的比例。如果不考虑遮挡，那么有效面积可能会超过总面积，这回造成BRDF不保能量，甚至可能会很明显，如下图所示：

在上半部分，平的宏表面为绿色，粗糙的微观表面为蓝色。m = h的microfacet标记为红色。宏表面投到视线方向就是左上角的绿线。同时，投出来的单个红色的microfacet显示成独立的红线。左下图表示在没有遮挡项的情况下，红色的microfacet加起来的面积，结果就是有效面积大于总面积，所以BRDF的反射能量错误地大于了接收能量。右下图里红色区域考虑了遮挡，重叠的区域不再计算多次，所以有效面积小于总面积。

对比

游戏中常用的的反射方程是这样的：

根据前面所述，(n · l_c)实际上是属于反射方程，而不是diffuse，所以应该改成：

其中，r_v是视线方向对法线的反射向量，来自Phong模型。但是上一篇文章所论述的microfacet BRDF中并没有这一项。Blinn-Phong模型的形式和它类似，但用的是更有物理意义的h，也就是microfacet的m。改用Blinn-Phong的话就得到：

从前面提到的Lambert可以发现，diffuse项已经和基于物理的一样了：

所以，现在我们专注于specular项，前面的公式如果只看specular是这样的

比较microfacet specular：

首先，从公式可以看出，游戏中用的c_spec应该用表示Fresnel的F(c_spec, l_c, h)替换。

第二，上文说过，D(h)与粗糙度有关，所以可以认为D(h)和Blinn-Phong的(n · h)^α功能相似。但是，要把(n · h)^α替换成正确的microfacet分布函数，就必须做一个归一化。也就是说，对于任意的视线方向v，微表面投影的面积之和必须等于宏表面投影的面积，数学上就是：

既然这个方程是对任何视线方向都得成立，那么对于特殊情况v = n也得成立：

Blinn-Phong的项如果也要满足这个方程，就得乘上一个归一化系数：

现在剩下的一项，就是：

这个项的物理意义是可见性（遮挡项除以校正因子）。我们修改过的specular模型并不打算包含可见性，所以简单地把这个项设成1就行了，也就是：

实际上，这对于仅包含height field的微表面是成立的（Blinn-Phong的表面分布函数也对应于此，因为所有背面的microfacet都等于0）。当l = n而且v = n的时候G_implicit()等于1, 这对于height field也是正确的（在宏表面的法线方向没有任何遮挡）。对于很斜的视角或者很斜的光线角都趋向于0，这也是正确的（microfacet被其他microfacet遮挡的可能性随着视角的增加而增加）。

经过整理，来自microfacet specular BRDF的几个项都明朗了，于是得到下面的渲染模型：

前面的系数是因为((α + 2) / 2π) * (π / 4) = (α + 2) / 8。

把diffuse加回去，就得到：

这就是本系列文章最终推出的基于物理的渲染模型。对比原先游戏中使用的模型，计算量增加非常少，但不但保证了保能量，还能让美术更容易调整参数。

未来的工作

一个没有解决的问题是specular的power很高，而且非常光滑的表面。这样的材料对于渲染湿的表面这样的东西很重要。但是，精确光源的近似在这种情况下会挂掉，结果就是产生subpixel大小的极端强烈的高光，很不自然。实际上这种情况需要的是反射出光源的形状，这需要快到适合在游戏中使用的面光源近似。

另一个问题是有很多中geometry项，有没有能比G_implicit提供更好的视觉效果，同时开销很小的函数？候选之一是Kelemen et. al提出的，是对Cook-Torrance的geometry项的近似，但计算开销很小：

其中的(l_c · h)在Fresnel项中就有，可以重复利用。这个很接近完整的Cook-Torrance的geometry项除掉校正因子。

第三个问题是diffuse项的Fresnel。在现实中，没有“不带specular的表面”，这样的材质实际上c_spec值在0.03-0.06之间，而且α的值非常小（0.1-2.0之间）。在很斜的角度下，即使最粗糙的表面也有感觉得到的specular。缺乏这种效果是另一种游戏看起来不真实的原因。